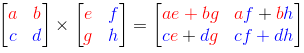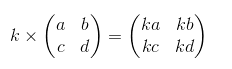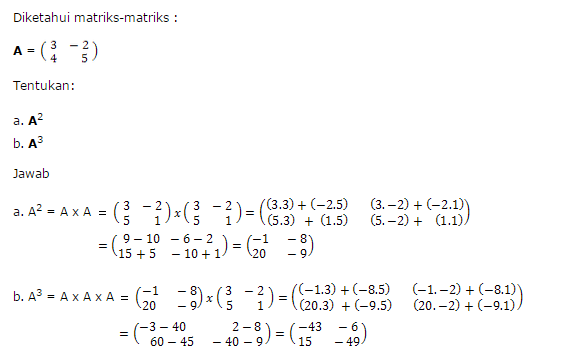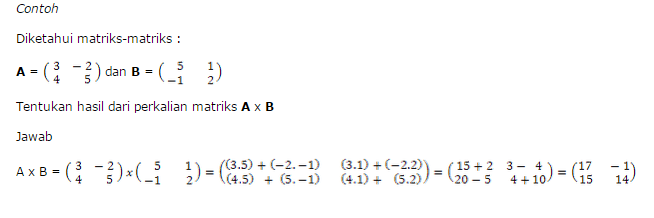Metode gauss CP3 Aljabar Linear

Coding phyton 2 library numpy


 numpy as np

def GENP(A, b):
    '''
    Gaussian elimination with no pivoting.
    % input: A is an n x n nonsingular matrix
    %        b is an n x 1 vector
    % output: x is the solution of Ax=b.
    % post-condition: A and b have been modified.
    '''
    n =  len(A)
    if b.size != n:
        raise ValueError("Invalid argument: incompatible sizes between A & b.", b.size, n)
    for pivot_row in xrange(n-1):
        for row in xrange(pivot_row+1, n):
            multiplier = A[row][pivot_row]/A[pivot_row][pivot_row]
            #the only one in this column since the rest are zero
            A[row][pivot_row] = multiplier
            for col in xrange(pivot_row + 1, n):
                A[row][col] = A[row][col] - multiplier*A[pivot_row][col]
            #Equation solution column
            b[row] = b[row] - multiplier*b[pivot_row]
    print A
    print b
    x = np.zeros(n)
    k = n-1
    x[k] = b[k]/A[k,k]
    while k >= 0:
        x[k] = (b[k] - np.dot(A[k,k+1:],x[k+1:]))/A[k,k]
        k = k-1
    return x

def GEPP(A, b):
    '''
    Gaussian elimination with partial pivoting.
    % input: A is an n x n nonsingular matrix
    %        b is an n x 1 vector
    % output: x is the solution of Ax=b.
    % post-condition: A and b have been modified.
    '''
    n =  len(A)
    if b.size != n:
        raise ValueError("Invalid argument: incompatible sizes between A & b.", b.size, n)
    # k represents the current pivot row. Since GE traverses the matrix in the upper
    # right triangle, we also use k for indicating the k-th diagonal column index.
    for k in xrange(n-1):
        #Choose largest pivot element below (and including) k
        maxindex = abs(A[k:,k]).argmax() + k
        if A[maxindex, k] == 0:
            raise ValueError("Matrix is singular.")
        #Swap rows
        if maxindex != k:
            A[[k,maxindex]] = A[[maxindex, k]]
            b[[k,maxindex]] = b[[maxindex, k]]
        for row in xrange(k+1, n):
            multiplier = A[row][k]/A[k][k]
            #the only one in this column since the rest are zero
            A[row][k] = multiplier
            for col in xrange(k + 1, n):
                A[row][col] = A[row][col] - multiplier*A[k][col]
            #Equation solution column
            b[row] = b[row] - multiplier*b[k]
    print A
    print b
    x = np.zeros(n)
    k = n-1
    x[k] = b[k]/A[k,k]
    while k >= 0:
        x[k] = (b[k] - np.dot(A[k,k+1:],x[k+1:]))/A[k,k]
        k = k-1
    return x

if __name__ == "__main__":
    A = np.array([[1.,-1.,1.,-1.],[1.,0.,0.,0.],[1.,1.,1.,1.],[1.,2.,4.,8.]])
    b =  np.array([[14.],[4.],[2.],[2.]])
    print GENP(np.copy(A), np.copy(b))
    print GEPP(A,b)

Read More

Program Aljabar Matriks dan Metode

Hello sobat semua pasti penasaran sama Program Matrix kali ini :) atau ada tugas dari dosen suruh buat program matrix? Berikut codingan Program Matrix menggunakan Bahasa Pemrograman Python yang berisi : Determinan, Ekspansi, Kofaktor

def banner():
    print("Menghitung invers matriks 3x3")
    print("CP Aljabar dan Linier")

def determinan():
    global det
    det = (bar1[0] * bar2[1] * bar3[2]) + (bar1[1] * bar2[2] * bar3[0]) + (bar1[2] * bar2[0] * bar3[1]) - (bar1[2] * bar2[1] * bar3[0]) - (bar1[0] * bar2[2] * bar3[1]) - (bar1[1] * bar2[0] * bar3[2])
    print("Nilai determinannya adalah: ",det)
    hitung()

def hitung():
    m11 = (bar2[1] * bar3[2]) - (bar2[2] * bar3[1])
    m12 = (-1 * ((bar2[0] * bar3[2]) - (bar2[2] * bar3[0])))
    m13 = (bar2[0] * bar3[1]) - (bar2[1] * bar3[0])

    m21 = (-1 * ((bar1[1] * bar3[2]) - (bar1[2] * bar3[1])))
    m22 = (bar1[0] * bar3[2]) - (bar1[2] * bar3[0])
    m23 = (-1 * ((bar1[0] * bar3[1]) - (bar1[1] * bar3[0])))

    m31 = (bar1[1] * bar2[2]) - (bar1[2] * bar2[1])
    m32 = (-1 * ((bar1[0] * bar2[2]) - (bar1[2] * bar2[0])))
    m33 = (bar1[0] * bar2[1]) - (bar1[1] * bar2[0])

    print("\n\n Kofaktor matriks adalah")
    print("|", m11, m12, m13, "|")
    print("|", m21, m22, m23, "|")
    print("|", m31, m32, m33, "|")

    print("\n\n Adjoin matriks")
    print("|", m11, m21, m31, "|")
    print("|", m12, m22, m32, "|")
    print("|", m13, m23, m33, "|")

    if det == 0:
        print("Tidak bisa dibagi dengan determinan 0")
        exit()

    print("\n\n Invers matriks")
    print("|", m11/det, m21/det, m31/det, "|")
    print("|", m12/det, m22/det, m32/det, "|")
    print("|", m13/det, m23/det, m33/det, "|")

banner()
print("Silahkan masukan elemen matriks, untuk kolom kedua dan ketiga dipisahkan dengan spasi")
print("contoh :2 4 5")
str_arr = input("Silahkan masukan baris pertama: ").split(' ')
bar1 = [int(num) for num in str_arr]

str_arr = input("Silahkan masukan baris kedua  : ").split(' ')
bar2 = [int(num) for num in str_arr]

str_arr = input("Silahkan masukan baris ketiga : ").split(' ')
bar3 = [int(num) for num in str_arr]

print("|",bar1,"|")
print("|",bar2,"|")
print("|",bar3,"|")

determinan()

contoh hasil :

Read More

Rumus Perkalian Matriks dan Perkalian Skalar Matriks

Rumus Perkalian Matriks

Operasi cara mencari rumus perkalian matriks matematika mempunyai metode rumus menghitung matriks yang sangat berbeda dengan operasi menghitung nilai penjumlahan atau pengurangan matriks.

Metode yang diterapkan di dalam rumus menghitung perkalian matriks ialah dengan memasangkan baris pada matriks pertama dengan kolom pada matriks kedua tetapi kedua nilai matriks ini bisa di kalian jika banyak kolom pada matriks pertama mempunyai nilai yang sama dengan banyak baris pada matriks kedua dan hasil perkalian matriks akan mempunyai baris yang sama banyak dengan baris matriks pertama.

Bagan Rumus Perkalian Matriks

Rumus Perkalian Matriks Skalar

Sedangkan untuk penjelasan dari rumus perkalian skalar matriks dilakukan dengan cara konstanta yang artinya nilai matriks bisa dikalikan dengan cara mengalikan setiap eleman atau komponen nilai matriks dengan skalar. Misalnya nilai Matriks A dikalikan dengan skalar K maka setiap eleman atau komponen Matriks A dikali dengan k.

Rumus Perkalian Matriks Skalar

Contoh Soal Perkalian Matriks

Hanya seperti itulah penjelasan yang bisa kami berikan kepada anda semua dan semoga penjelasan Rumus Menghitung Perkalian Matriks dapat berguna dan bermanfaat bagi anda semuanya baik siswa atau siswi maupun para mahasiswa karena tujuan kami dalam penulisan ini ditujukan untuk kalian semuanya.

Read More

MATRIKS

Matriks adalah sekumpulan bilangan yang disusun dalam sebuah empat persegi panjang, secara teratur, di dalam baris-baris dan kolom-kolom.

Gambar Matriks

Matriks di atas disebut matriks ukuran m x n

Operasi-operasi pada Matriks

1. Kesamaan Dua Buah Matriks

 Dua matriks A dan B disebut sama, jika ukurannya sama dan berlaku : [ aij ] = [ bij ]

A = B

A ≠ C

B ≠ C

2. Penjumlahan dua matriks

 Jumlah dua buah matriks A + B bisa dilakukan asalkan kedua matriks tersebut berukuran sama

Sifat-sifat penjumlahan:

Komutatif : A + B = B + A

Assosiatif : A + (B + C) = (A + B) + C

3. Perkalian Matriks dengan Skalar

 Jika k suatu skalar, maka matriks kA = (kaij)

Diperoleh dengan mengalikan semua elemen matriks A dengan k

4. Pengurangan Matriks

 Mengurangi matriks A dengan B (A-B) adalah menjumlahkan matriks A dengan matriks (-B)

5. Perkalian Matriks

 Syarat perkalian matriks : banyaknya kolom matriks pertama = banyaknya baris matriks kedua.

Hasil perkalian antara matriks A = [aij] berordo mxp, dengan matriks B = [bij] berordo pxn, adalah matriks C = [Cij] berordo mxn.

Read More

Determinan dan Matriks Singular + metode sarrus

Determinan dan Matriks Singular 

Untuk kepentingan praktis, penting untuk mengetahui apakah suatu matriks memiliki invers atau tidak. Untuk itu, kita akan mendiskusikan satu operasi tambahan pada matriks persegi, yang disebut determinan. Untuk matriks 1 × 1 determinannya adalah elemennya itu sendiri. Untuk matriks 2 × 2,

determinan dari A, ditulis sebagai det(A) atau dinotasikan dengan garis-garis vertikal |A|, dapat dihitung sebagai selisih dari perkalian diagonal-diagonalnya, dimulai dengan elemen-elemen pada diagonal kiri-atas:

Determinan Matriks 2 × 2Diberikan sebarang matriks 2 × 2,

det(A) = |A| = a11a22 – a21a12.

Contoh 1: Menghitung Determinan

Hitunglah determinan dari masing-masing matriks yang diberikan.

Pembahasan Matriks B adalah matriks persegi dengan ordo 2 × 2, sehingga

Sedangkan matriks C bukan matriks persegi, padahal determinan suatu matriks didefinisikan hanya untuk matriks persegi, sehingga C tidak memiliki determinan. Selanjutnya, determinan dari matriks persegi D adalah sebagai berikut.

Perhatikan bahwa determinan dari matriks D adalah nol dan matriks ini sama dengan matriks yang telah kita selidiki sebelumnya bahwa matriks tersebut tidak memiliki invers. Hal ini dapat kita gunakan untuk matriks yang lebih besar dan memberikan hubungan antara suatu matriks, inversnya, dan persamaan matriks.

Matriks Singular
Jika A adalah matriks persegi dan det(A) = 0, maka invers dari matriks tersebut tidak ada dan A dikatakan sebagai singular atau non-invertibel.

Secara singkat, invers hanya ada untuk matriks persegi, tetapi tidak semua matriks persegi memiliki invers. Jika determinan dari suatu matriks persegi sama dengan nol, maka invers dari matriks tersebut tidak ada dan metode persamaan matriks tidak dapat digunakan untuk menyelesaikan sistem persamaan linear.

Pada pembahasan yang lalu kita sudah membahas tentang cara mencari determinan matriks yang berordo 2 x 2. Sekarang pembahasannya kita lanjutkan tentang bagaimanakah mencari determinan suatu matriks yang berordo 3 x 3?. Sebenarnya ada beberapa cara untuk mencari determinan matriks, tetapi untuk pembahasan kita kali ini kita hanya akan membahas tentang menghitung determinan matriks yang berordo 3 x 3 dengan memakai metode sarrus.

Baik sebelum kita lanjut ke materi pokok, kita berkenalan dulu dengan struktur matriks berordo 3 x 3. Apa sih yang dimaksud dengan matriks yang berordo 3 x 3?. Matriks 3 x 3 artinya matriks yang jumlah barisnya sebanyak tiga dan jumlah kolomnya juga sebanyak tiga. Secara lengkap matriks 3 x 3 bisa dilihat di bawah ini :

• 

Soal 1# :

Tentukanlah determinan dari matriks berikut :

Jawaban :

Untuk menentukan determinannya, terlebih dahulu kita keluarkan dua kolom pertamanya, sehingga matriks tersebut menjadi :

Kemudian yang segaris kita kalika dan tandanya mengikuti aturan yang di atas

Det A = 2.4.1 + 3.3.7 + 4.5.0 – 4.4.7 – 2.3.0 – 3.5.1

Det A = 8 + 63 + 0 – 112 – 0 – 15 = – 56

Jadi determinan matriks tersebut adalah -56.

Read More